

They should increase their abilities to visualize, describe, and analyze situations in mathematical terms.

… students should build on their prior knowledge, learning more varied and more sophisticated problem-solving techniques. The NCTM states in Principles and Standards for School Mathematics (PSSM): In the later grades, students have the opportunity to enlarge on these earlier studies. Students should solve problems in which they use tables, graphs, words, and symbolic expressions to represent these functions and patterns of change. How many days will the business need to operate before revenue equals cost? This system involves the following equations:10,000 + 1,000x = yĪccording to the National Council of Teachers of Mathematics (NCTM), the study of mathematical patterns and relationships in the middle grades should focus on patterns that relate to linear functions – that is, functions that arise when there is a constant rate of change. The costs for the same business consist of a fixed amount of $10,000 and a flexible amount of $1,000 per day. The revenue for a certain business is $2,500 per day.How many miles (x) would one have to drive before the total cost (y) of driving Car A and Car B would be the same? This system involves the following equations:25,000 +. Car B costs $18,500 to purchase and 40 cents a mile to drive. Car A costs $25,000 to purchase and 35 cents a mile to drive.In Algebra 1, students are usually taught the graphing method, the substitution method, and the linear combination method. If the two lines are parallel, there is no solution (this system is called inconsistent).Īdditional methods of solving the system include substitution, linear combinations, determinants (Cramer’s Rule), and matrices. If the two lines are on top of one another, there are an infinite number of solutions, because each point on the line is considered a solution (this system is called dependent). If the lines intersect at exactly one point, there is one solution to the system, and the system is called consistent. One method is to graph the equations as two lines and examine them. Systems of linear equations can be solved using a variety of methods.
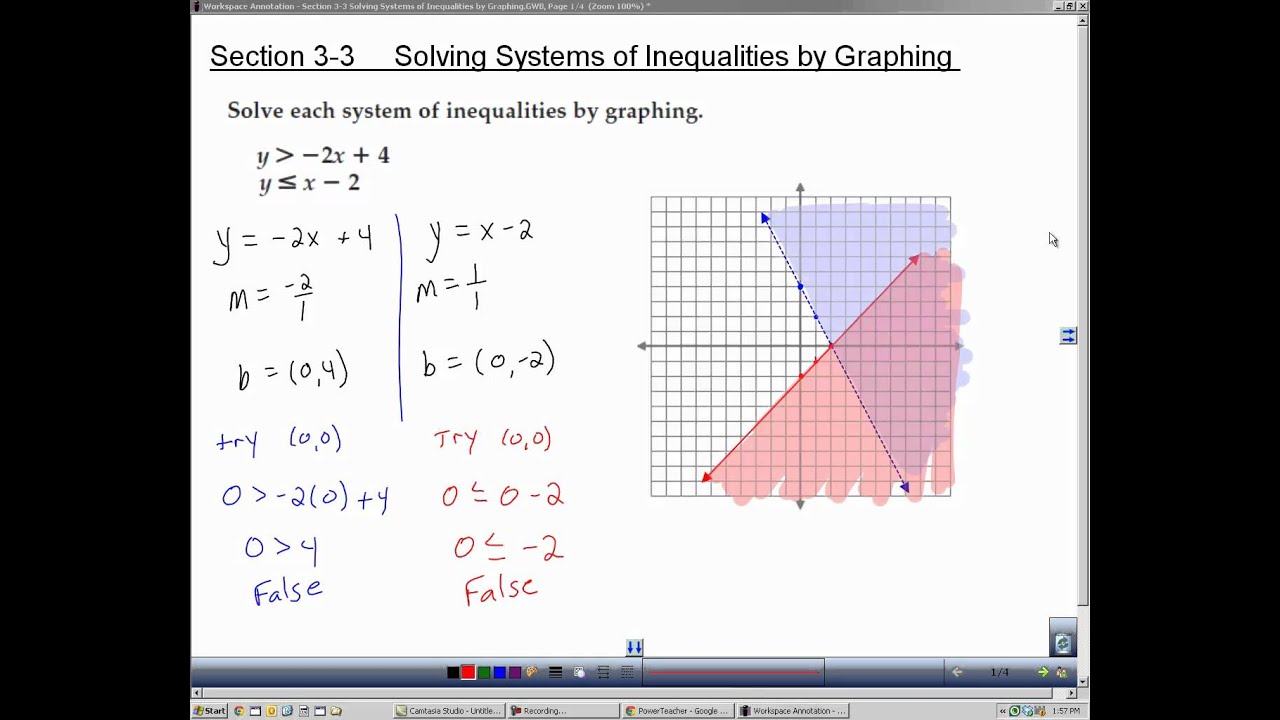
To solve a system means to find the x- and y-values for which both of the equations are true. Examining the cost of video rentals at two different stores as a function of the number of videos rented, or looking at the monthly cost of two cell phone plans as a function of minutes used are examples of systems of equations. Solving a system of equations can be useful in calculating the cost difference between various payment plans, or in figuring out when a business enterprise will break even. In order to “solve the system,” students must find values for the variables that make both statements true. For example, the equations 2x + 3y = 4 and 3x + 4y = 5 form a system if x represents the same thing in both equations, y represents the same thing in both equations, and both equations refer to the same context. A system of equations consists of two or more equations that have variables that represent the same items.


 0 kommentar(er)
0 kommentar(er)
